A quick update for Lighthouse; current progress, fork choices, mono-repos, BLS libraries and things to come.

Summary

This update primarily focuses on a high level discussion on some of the technical aspects that we've dealt with recently for Lighthouse. In particular, we look at fork-choice algorithms, BLS libraries and the pros/cons of maintaining a mono-repo. In addition, we document the technical progress being made in Lighthouse, in particular:

• Implementation and testing of a number of fork-choice rules.
• BLS implementation passing test-vectors.
• Generation of test vectors for the new get_permuted_index shuffling function.
• Updating the codebase to spec v0.2.0 release.
• Deciding to maintain a large mono-repo for Lighthouse.
• Starting fuzzing basic types supported by SSZ.
• Preparation of a presentation for Mehdi to give at EthCC on the 6th of March.

Fork Choice

What is a fork choice?

Under normal running conditions (even without any bad actors) it is natural for a blockchain to deviate from a single, long, canonical chain of truth; often multiple blocks are created that have the same parent. This commonly arises as a consequence of network latency -- a solved block might not reach a miner before it finds an alternative solution itself.

When the nodes on the network disagree upon which block is canonical, we say the network has forked. Note, this is different to what is commonly referred to as a "hard-fork" which is the result of software upgrades.

To resolve a fork and regain consensus, we require a method for deciding which chain of blocks is going to be the "correct" chain and which we will be discarded. The algorithm that makes this decision is called the fork-choice algorithm. A simple solution commonly utilised in Proof of Work (PoW) chains is to pick the chain with the most blocks (a.k.a. the "longest" chain). This works well for PoW systems as it takes work to create a block and thus the longest chain represents the most work done. See the diagram below.

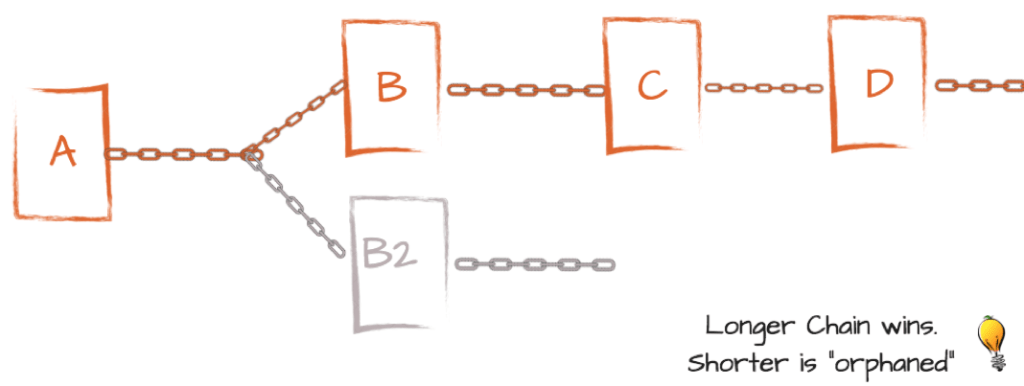This image is from Shawn Dexter's post which is a good resource for understanding the longest-chain fork choice rule.

Fork Choice in Serenity

Serenity uses Proof of Stake (PoS), which means it has a set of validators who vote on the blocks they think are "correct" instead of miners that perform proof-of-work. We can no longer use the simplistic longest chain strategy as the longest chain no longer represents the most valuable chain. Instead, we must instead select the chain which earned the most votes from validators in the system.

In Serenity, the fork-choice algorithm is called the Latest-Message-Driven Greediest Heaviest Observed Sub-Tree, or LMD-GHOST for short. In essence, it chooses the chain which has the most votes based on the most recent collection of votes from the validators (a vote for a current block also counts as a vote for its parent, grand-parent, great-grandparent, etc.).

Currently, there is a sub-optimal, computationally expensive implementation of LMD-GHOST in the current spec, alongside a number of more optimal implementations which we have explored recently. In particular, Vitalik has created an optimised version of bitwise LMD-ghost, the Python code for which can be found here. In addition, @Protolambda has been working on a variety of optimised implementations for LMD-GHOST which can be found in his lmd-ghost repository. Each of these implementations have their own pros and cons with regards to computational efficiency.

As there can be many validators voting on a range of different forks, this algorithm can easily become computationally expensive. Since it must be executed regularly, it can become a significant consumer of client resources and a potential DoS vector.

As some implementations may be more optimal for particular circumstances than others (e.g. large/small number of active validators), Lighthouse has implemented a few of these fork-choice rules in a swappable manner so the most efficient implementation can be used given the state of the ecosystem at the time.

Mono Repository vs Multi Repository

Currently, the Lighthouse repository hosts a number of distinct elements and consideration was given to splitting these out into their own repositories. There is the beacon node binary, the validator client (a separate binary that connects to beacon nodes) and an Eth 2.0 library which contains a variety of crates and utilities that implement the Serenity spec and are used by both the validator client and the beacon node.

Initially, it was thought that separating these out into separate repositories would be beneficial as it gives distinct and clear version control over the libraries and binaries. Furthermore, it would clearly separate project management tasks, i.e. having distinct Github issues and pull requests on each project. However after some experimentation, we have decided to stick with a single, mono-repository for now. Along with some of the points mentioned in this article, we decided that the multi-repo approach causes more issues than it addresses, at least at this stage. In particular, the Eth 2.0 library is not stable and often requires updates. Due to inter-dependencies between the binaries and this library, updating the library would often involve multiple commits updating the library, then the binaries, then the library again. We would also require multiple build scripts for each repository to build their respective code, which adds additional overhead. Perhaps in the future, once the library crates become stable, we will segregate these out into their own repository that can be managed separately. For the time being, the validator client, the beacon-node and all related libraries will be managed in a single repository, Lighthouse.

BLS Basics

The BLS signature scheme used by Serenity is a bilinear pairing scheme. Even at a high level, there are a few important mathematical concepts required to explain how the scheme works. First is the bilinear pairing, that is, given two finite groups (generated from elliptic curves in BLS) $G_1$ and $G_2$ we can pair two points together to lie in a third group $G_T$ (i.e $(G_1, G_2) \rightarrow G_T$). Second, given a generator (a predefined point on the curve) we can multiply it by an integer (the secret key, $P_{secret}$) to get another point (the public key, $P_{public}$). Then given this point and the generator it is hard to find the multiplicator (i.e. secret key, $P_\text{secret}$). For Serenity we use public keys as points on $G_1$ hence we use the generator on $G_1$ (for simplicity, let's call this point, $G$). Thus we have,

$$P_{public} = G^{P_{secret}}$$

In BLS, a signature is also a point on a curve however it is from the other group $G_2$. To get a signature we hash the message to be signed and convert that to a point on $G_2$ (we call this point $M_{G_2}$). Then we multiply this by the secret key.

$$signature = M_{G_2}^{P_\text{secret}}$$

To verify a signature we use two pairings between $G_1$ and $G_2$ and ensure they match,

$$\text{pairing}(G, signature) == \text{pairing}(P_\text{public}, M_{G_2})$$

This process can also be extrapolated using aggregation which allows an aggregate public key to represent a combination of public keys, and an aggregate signature to represent a combination of signatures (provided the message is the same). This is a convenient way of compressing a large number of public keys and signatures down to a single point for each. This compression of signatures is crucial for serenity to reduce bandwidth and computation requirements across the network.

If you'd like a more detailed explanation visit here.

Currently (though subject to change), Serenity is planning to use $G_1$ points (48 bytes compressed) as the public keys and $G_2$ points (96 bytes compressed) for signatures, which is the reverse of Zcash's implementation. The reasoning behind this is likely due to the large number of public keys required to be stored in the beacon chain, and choosing $G_1$ points as public keys halve the space requirements.

The sigp/signature-schemes library (unsafe) has now been updated to version 0.5.2 which now passes the test vectors set out in Eth 2.0. What this means is that given a secret key, our signature scheme will give the same public key. Given a message, you'll hash to the same point on $G_2$, and given a message and secret key you'll get the same signature. This process involved switching the $G_1$ and $G_2$ curves, writing the mapping function from a message to a $G_2$ point, and producing tests to be run against a given YAML test-vector file. Feel free to check out and test this library which can be found here: github.com/sigp/signature-schemes.

The Road Ahead

In the coming weeks, we are beginning the implementation of our networking infrastructure using the Gossipsub protocol, which we previously developed for rust-libp2p. This will inevitably be a detailed process which will lead us towards the March testnet, and will hopefully see improvements to the gossipsub libp2p implementation. Client interoperability (on the networking side) will also be in scope and we should expect to see the Gossipsub Rust implementation change to align with other implementations of libp2p.

As always we will be updating the codebase according to the spec and be looking at simple optimisations already in the code base.

For further updates, remember to catch Mehdi's talk at EthCC on the 6th of March!

Contributors

As always, we're keen for more contributors! If you want to get involved, please find a "good-first-issue" and leave a comment or drop us a line on the gitter channel.