Unraveling a Curious Edge Case in EigenLayer's Slashing Accounting

NOTE: This post assumes that you already have a good understanding of EigenLayer's restaking protocol and M4 smart contracts (before the introduction of the slashing upgrade).

EigenLayer's slashing mechanism is an integral component of their restaking protocol, as it keeps AVS operators in check. The slashing mechanism introduced in ELIP-002 brings several new concepts to the EigenLayer restaking protocol that work together to create a robust slashing system that can handle both EigenLayer-native slashing and beacon chain slashing events.

In this post, we'll explore an interesting edge case discovered in this mechanism that affects how withdrawable shares are calculated under specific circumstances. But first, let's get a basic understanding of the slashing upgrade.

A Brief Explanation of EigenLayer's Slashing Upgrade

A detailed explanation of EigenLayer's slashing mechanism can be found in ELIP-002.

For the purpose of understanding this post, we will briefly cover how withdrawable shares are calculated.

There are three important factors that work together to determine a staker's "withdrawable shares":

Deposit Scaling Factor (DSF) - A per-staker, per-strategy value that scales a staker's deposit shares as they deposit assets over time. This factor helps account for slashing that may have occurred between deposits, so that new deposits are not penalised for previous slashing events. This increases as new deposits are made after slashing events, and resets when the staker delegates to a new operator or increases their deposit shares from zero.
Max Magnitude (MM) - This represents the proportion of an operator's delegated stake that remain unslashed after EigenLayer-native slashing in an operator set. An AVS slashes their operators by reducing their max magnitudes in a certain operator set. This monotonically decreases over time as the operator is slashed.
Beacon Chain Slashing Factor (BCSF) - This represents the proportion of a staker's beacon chain ETH that remains unslashed after slashing events on the beacon chain. This monotonically decreases over time as the staker's beacon chain ETH is slashed.

NOTE: You may also come across the Slashing Factor (SF). This is simply the product of the MM and the BCSF. It represents the proportion of a staker's deposit shares that remain unslashed after both EigenLayer-native slashing and beacon chain slashing.

The withdrawable shares for a staker can be calculated using this formula:

$$\text{withdrawableShares} = \text{depositShares} \times \text{DSF} \times \text{MM} \times \text{BCSF}$$

This mechanism has two interesting intertwined quirks:

AVS slashings and beacon chain slashings are handled independently of each other, but both are applied on the same deposit shares. This means that it is possible for the same shares to be slashed twice (once by an AVS and once by the beacon chain).
AVS slashings are in the the form of percentages, while beacon chain slashings are in the form of absolute ETH values (denominated in gwei). This may make it unclear how much ETH is being slashed. For example, considering a 32 ETH initial balance, an AVS slash of 50% of MM then a beacon chain slash of 16 ETH results in a withdrawable shares amount of 8 ETH, even though the staker already has 16 withdrawable ETH before the beacon chain slash. This is because 8 of the 32 ETH has been slashed twice.

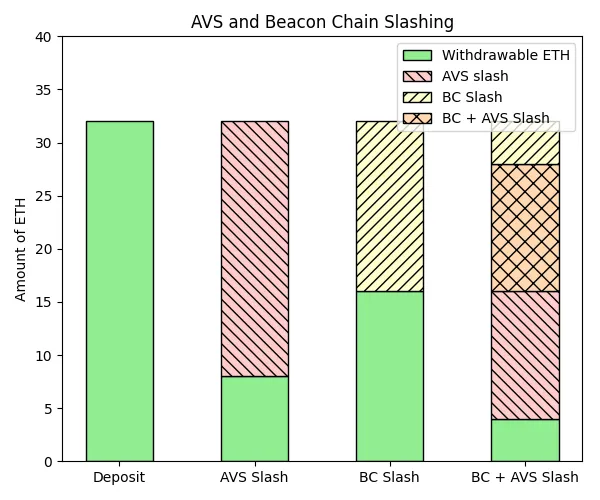
AVS and Beacon Chain Slashing Visualization — **Figure 1:** A visualization of how AVS slashing and beacon chain slashing can affect the same stake, leading to double slashing of the same ETH.
Source: EigenLayer Contracts Docs

The Edge Case: Inconsistent Withdrawable Share Calculations

While investigating EigenLayer's code, we discovered an interesting edge case in the beacon chain slashing factor calculation that can lead to inconsistent withdrawable share calculations depending on when validators are verified relative to checkpoints.

The root cause is in the _reduceSlashingFactor() function in EigenPodManager.sol:

function _reduceSlashingFactor(
    address podOwner,
    uint256 prevRestakedBalanceWei,
    uint256 balanceDecreasedWei
) internal returns (uint64) {
    uint256 newRestakedBalanceWei = prevRestakedBalanceWei - balanceDecreasedWei;
    uint64 prevBeaconSlashingFactor = beaconChainSlashingFactor(podOwner);
    // newBeaconSlashingFactor is less than prevBeaconSlashingFactor because
    // newRestakedBalanceWei < prevRestakedBalanceWei
    uint64 newBeaconSlashingFactor =
        uint64(prevBeaconSlashingFactor.mulDiv(newRestakedBalanceWei, prevRestakedBalanceWei));
    uint64 beaconChainSlashingFactorDecrease = prevBeaconSlashingFactor - newBeaconSlashingFactor;
    _beaconChainSlashingFactor[podOwner] =
        BeaconChainSlashingFactor({slashingFactor: newBeaconSlashingFactor, isSet: true});
    emit BeaconChainSlashingFactorDecreased(podOwner, prevBeaconSlashingFactor, newBeaconSlashingFactor);
    return beaconChainSlashingFactorDecrease;
}

As mentioned in the previous section, beacon chain slashings are handled independently of AVS slashings. Hence, the BCSF calculation does not take into account MM or DSF, and only uses balances as reported on the beacon chain.

Since the DSF is not factored into the BCSF calculation, the BCSF can be reduced too aggressively when a validator is slashed on the beacon chain after the staker has been slashed by an AVS.

A Practical Example

This edge case might be a bit confusing, so let's break it down with a practical example and note down any changes to the withdrawable shares and factors after each step.

Consider the following scenario:

A staker has staked and verified one validator in their EigenPod
They have been slashed by an AVS for 75% of their allocation
Their validator has been slashed on the beacon chain for 16 ETH, but they have not performed a checkpoint yet on the EigenPod
They plan to stake and verify a second validator in their EigenPod

Scenario A: The second validator is staked and verified AFTER the EigenPod checkpoint

Stake and verify the first validator (withdrawableShares = 32 ETH)
Slash operator for 75% of allocation (withdrawableShares = 8 ETH, MM = 0.25)
Slash the first validator for 16 ETH on the beacon chain
Perform an EigenPod checkpoint (withdrawableShares = 4 ETH, BCSF = 0.5)
Stake and verify the second validator (withdrawableShares = 36 ETH, DSF = 4.5)

where:

\begin{aligned} \text{DSF} &= \frac{\text{newWithdrawableShares}}{\text{newDepositShares} \times \text{SF}_{\text{stepFour}}} \\ &= \frac{36}{64 \times (0.25 \times 0.5)} \\ &= 4.5 \end{aligned}

\begin{aligned} \text{finalWithdrawableShares}_\text{A} &= \text{depositShares} \times \text{DSF} \times \text{SF} \\ &= 64 \times 4.5 \times (0.25 \times 0.5) \\ &= 36 \end{aligned}

Scenario B: The second validator is staked and verified BEFORE the EigenPod checkpoint

Stake and verify the first validator (withdrawableShares = 32 ETH)
Slash operator for 75% of allocation (withdrawableShares = 8 ETH, MM = 0.25)
Slash the first validator for 16 ETH on the beacon chain
Stake and verify the second validator (withdrawableShares = 40 ETH, DSF = 2.5)
Perform an EigenPod checkpoint (withdrawableShares = 30 ETH, BCSF = 0.75)

where:

\begin{aligned} \text{DSF} &= \frac{\text{newWithdrawableShares}}{\text{newDepositShares} \times \text{SF}_{\text{stepTwo}}} \\ &= \frac{40}{64 \times 0.25} \\ &= 2.5 \end{aligned}

\begin{aligned} \text{finalWithdrawableShares}_\text{B} &= \text{depositShares} \times \text{DSF} \times \text{SF} \\ &= 64 \times 2.5 \times (0.25 \times 0.75) \\ &= 30 \end{aligned}

Interpreting the Practical Example Results

Notice that Scenario A and Scenario B give you different final withdrawable shares.

What's even more interesting is that Scenario B results in a final withdrawable shares that is less than 32 ETH, which is the increase in deposit shares after the second validator was staked and verified in step 4. This means that the ETH from the second validator is being slashed, even though it was technically not slashed by an AVS or the beacon chain.

To calculate the expected final withdrawable shares, we can split the deposit shares of the two validators and apply slashing on each validator separately. Since both the AVS and beacon chain slashings only applied to the deposit shares belonging to the first validator, we can calculate the expected final withdrawable shares as follows:

\begin{aligned} \text{finalWithdrawableShares}_{\text{expected}} &= \text{withdrawableShares}_{\text{validatorOne}} \\ &\quad + \text{withdrawableShares}_{\text{validatorTwo}} \\ &= \text{depositShares}_{\text{validatorOne}} \times \text{SF}_{\text{validatorOne}} \\ &\quad + \text{depositShares}_{\text{validatorTwo}} \\ &= 32 \times (0.25 \times 0.5) \\ &\quad + 32 \\ &= 36 \end{aligned}

We can see that Scenario A results in the expected final withdrawable shares amount.

EigenLayer's Response

EigenLayer acknowledged this edge case and decided to keep the current implementation. Not all is lost, though. Reporting this edge case gave them the opportunity to test their understanding of their design choices, and improve their documentation.

To summarise their response, the system intentionally reduces the attributable slashed amount for an AVS when beacon chain slashing occurs. Any differences in final withdrawable shares based on checkpoint timing are a natural consequence of the asynchronous beacon chain proof system.

To better illustrate this, consider that in Scenario B, the staker's slashed amount after AVS slashing in Step 2 is 24 ETH. After the EigenPod checkpoint in Step 5 captures a beacon chain slashing event of 25% of the total deposit shares (16 out of 64 ETH), the AVS-slashed amount is correspondingly reduced by 25% to 18 ETH.

Compare this to Scenario A, where the beacon chain slashing event is recorded as 50% of the total deposit shares (16 out of 32 ETH) since the second validator has not been verified yet, and the corresponding AVS-slashed amount is reduced by 50% to 12 ETH.

You might notice from the example above that a positive side effect of this behaviour is that it incentivises stakers to perform EigenPod checkpoints more frequently, as this reduces the amount of ETH that is slashed by the AVS.

Conclusion

Complex accounting is hard to get right. This means that for security researchers, it is also hard to understand and spot edge cases solely through manual code review. Hence, it's important to also test the code in many different scenarios to catch these edge cases.

Thank you to the EigenLayer smart contract and security team for their unwavering dedication to the security of their protocol.

For the full report and EigenLayer's response to this edge case, see the Further Readings section below.